The school year had barely begun, and I was already on the verge of shock. Let me explain – and I promise, this has a satisfying conclusion.
I had the privilege of collaborating with sixth-grade students, and I decided to use a lesson from Robert Kaplinsky, a resource that provides excellent context for understanding least common multiple. Interestingly, this particular lesson was inspired by one of my favorite movies, “Father of the Bride.” (Yes, I know, it took me long enough to blog about this, right?) To set the stage, this was my first time working with this teacher and her students at the beginning of the school year. I was new to them, and they were new to the concept of LCM. I showed the teacher Kaplinsky’s lesson, and she enthusiastically invited me to conduct it with her class. Here’s how it unfolded.
How Many Hot Dogs and Buns Should He Buy?
I implemented this lesson across three class periods, and I’d like to think it progressively improved with each session – a common teacher experience! This was my initial foray into Robert’s lesson plans, and I aimed to facilitate the activity in a manner similar to his approach, drawing upon his suggestions within the lesson outline.
First Attempt: Initial Questions and Unexpected Responses
I started by giving the students some context about the movie clip we were about to watch. I explained that George Banks (played by Steve Martin) is at the grocery store, preparing for a family dinner. In the movie, George is visibly stressed about the mounting expenses of his daughter’s wedding. Those familiar with “Father of the Bride” know that George Banks is, shall we say, extremely frugal and mindful of his spending.
After providing this background, I played the movie clip and posed the question to the students, “What questions do you have after watching this?” Hands shot up immediately, and I was encouraged. However, the questions I received were not quite what I anticipated:
- “Why is he wearing a suit?”
- “Why is he so angry?”
- “Who is that man?”
Hmm… these weren’t the mathematical inquiries I was expecting. So, I reframed my question: “What do you think we are trying to figure out in this situation?” The response? Silence. Strike one.
Trying a different angle, I asked, “Why is George so upset in the video?” A student finally responded, “Because there is a different number of hot dogs and hot dog buns in each package.” Yes! Maybe I’m not failing completely as a teacher…
“Interesting point. What would happen if he buys only one package of hot dogs and one package of hot dog buns?” A student quickly answered, “He would have 4 extra hot dog buns?” Correct! My success rate is improving!
“How would having extra buns make someone like George feel?” Students chimed in with, “Angry,” “Mad,” “Upset.” I’m feeling like a teaching rockstar right now!
“Okay, let’s help George avoid getting so upset. Let’s investigate this question: ‘How many packages of hot dogs and packages of hot dog buns should he buy so he doesn’t have any leftover?’”
I then introduced Robert’s Problem Solving Framework and guided the students to write the main question on their worksheets and make an initial guess. To enhance their engagement and sense of inquiry, I borrowed a strategy from Robert: I informed the students, “I will not give you any information about the problem unless you specifically ask for it.” Here’s what the class collaboratively brainstormed regarding what they knew and what they needed to know:
| What do you already know from the problem? | What do you need to know to solve the problem? |
|---|---|
| – One package contains 8 hot dogs. – One package contains 12 hot dog buns. – George is frugal (cheap). – His daughter is getting married. | – How many people are coming to dinner? – How much money does George has? – What is the price of one package of hot dogs? – What is the price of one package of hot dog buns? |
After confirming the information they already knew, I addressed each of their questions with a simple, “I don’t know.” I then added, “But remember, George is very frugal and doesn’t want to overspend.” With that, I let them work independently or in small groups. Many students approached the problem visually, as seen in these examples:
Student sample #1:
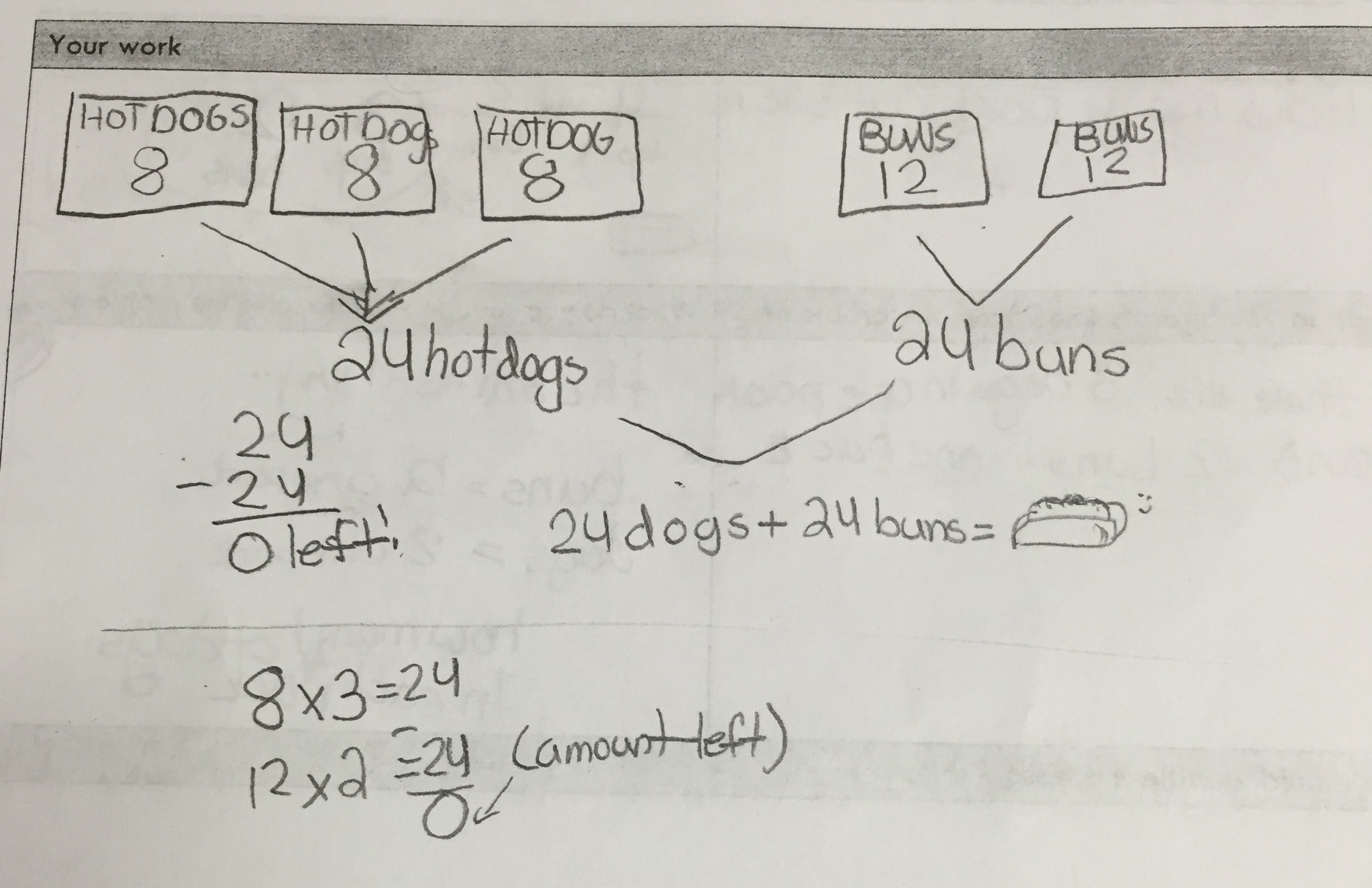student work sample showing groups of 8 and 12
Student sample #2:
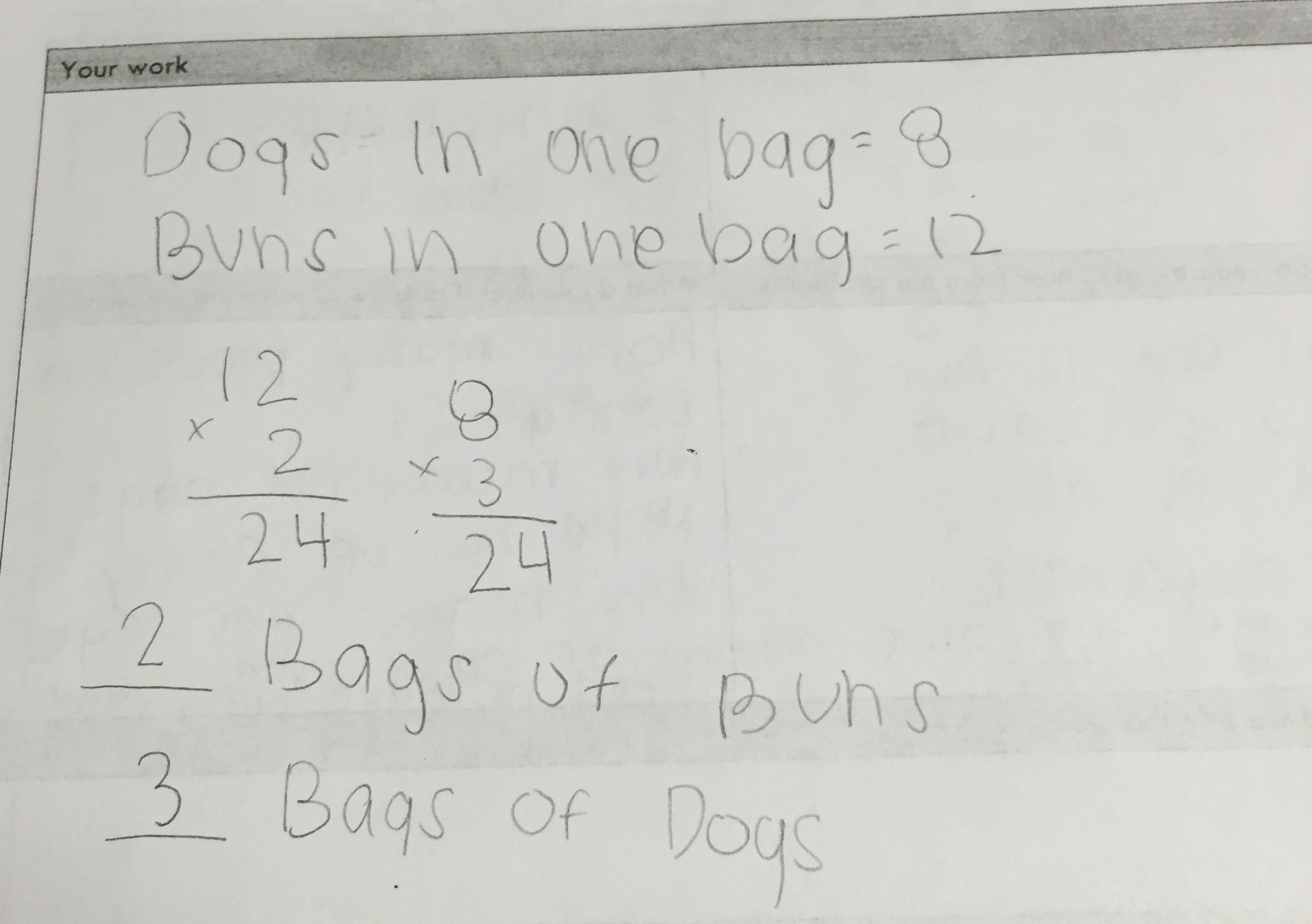student work sample showing addition of 8s and 12s
Student sample #3:
(This student’s comment was both funny and a little heartbreaking when I saw the struggle in the work at the top left…)
Overall, my first attempt felt successful. The students were actively discussing the problem, many were arriving at the correct answer, and we even tackled an extension question. In the extension, I asked them to consider how the solution would change if hot dog packages contained 10 hot dogs and bun packages contained 6 buns. I walked into the next class period with a revised strategy and a sense of optimism.
Second Attempt: Refining the Approach and Discovering Multiple Solutions
Based on my first experience, I decided to implement the following adjustments for the second class:
- Continue providing background information about the movie to set the context.
- Omit the initial broad questions like “What questions do you have?” or “What do you think we are trying to figure out?” to focus their thinking more directly.
- After the video clip, directly initiate the discussion with “Why is George so upset?” followed by “What would happen if he buys only one package of each?” to guide them towards the core problem.
- Maintain the use of the Problem Solving Framework, asking students to identify known and needed information.
- Allow students to solve the problem independently.
This second class started much more smoothly, and I felt a surge of confidence in my refined approach. The students’ list of knowns and unknowns was similar to the first class. Again, my response to their “need to know” questions remained “I don’t know.”
As I circulated around the room, a student’s question stopped me in my tracks: “Mr. Luevanos, can there be more than one answer?” Wait, what? I paused, resisting the urge to say no immediately, and instead asked, “Tell me more about what you’re thinking.” The student explained that the answer could change depending on the number of people coming to dinner. Looking around, I realized this insightful thinking was spreading among several students. I observed work like this:
Student sample #4:
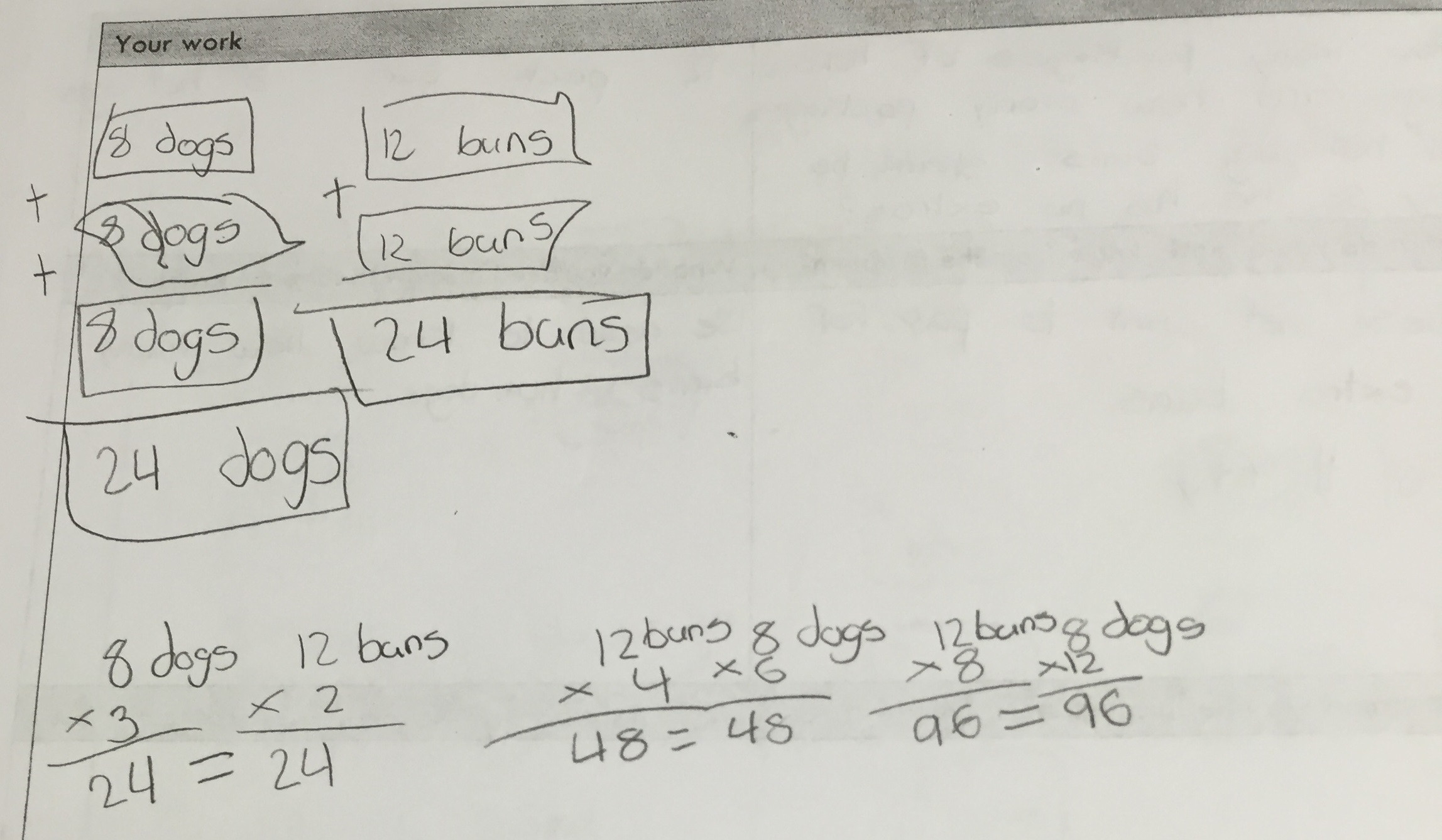student work showing multiples of 24, 48, 72
Student sample #5:
student work showing lists of multiples of 8 and 12
Student sample #6:
Are you thinking what I’m thinking?! O…M…G!
In that instant, the lyrics from “Van Halen II” echoed in my mind:
You better call up the ambulance, I’m deep in shock. Overloaded, baby, I can hardly walk. Somebody get me a doctor!
These students weren’t just finding one common multiple, they were discovering multiple common multiples of 8 and 12! Seeing their work and asking clarifying questions, I had a sudden, profound realization of the lesson’s true power. The possibility of multiple solutions hadn’t even crossed my mind initially, and now it was unfolding as a powerful learning opportunity.
It took every ounce of self-control to contain my excitement and maintain a calm demeanor. I asked these three students to share their strategies with the class, guiding the discussion with questions like:
What do the numbers 8 and 12 represent in the problem? Why are you adding 8 repeatedly here? Why are you adding 12 repeatedly? What does the number 24 represent in this context? How many packages of hot dogs and buns would George need for 24 hot dogs? Where can you see the number of packages in (student’s name)’s work?
Then, I dropped what felt like a teaching “mic drop” moment. Knowing there was more than one correct answer, and considering what they knew about George Banks’ character, I asked:
“Knowing that there is more than one correct answer, and remembering George Banks’ personality, which answer seems the most reasonable for him?”
Many students suggested 3 packages of hot dogs and 2 packages of hot dog buns, while some remained unsure.
“Why do you think that?” I probed.
“Well, it depends on how many people are coming to dinner,” one student offered.
“I think he’d only want to buy enough food for 24 hot dogs because he doesn’t like to spend money,” another added.
“Yeah! He’s cheap!” another student exclaimed, solidifying the connection.
“Oh yeahhhh!” the class echoed, as the understanding clicked.
“Hmm, interesting. You are all right. We don’t have enough information to know if he needs food for 24, 48, 96, or more hot dogs. But… based on what we do know about George, and that he is careful with his money, which of these scenarios do you think George would prefer to minimize waste and spending?”
The class overwhelmingly agreed that George would likely prefer to buy just 3 packages of hot dogs and 2 packages of hot dog buns. Here are further examples of student work demonstrating this understanding:
Student sample #6 (continued):
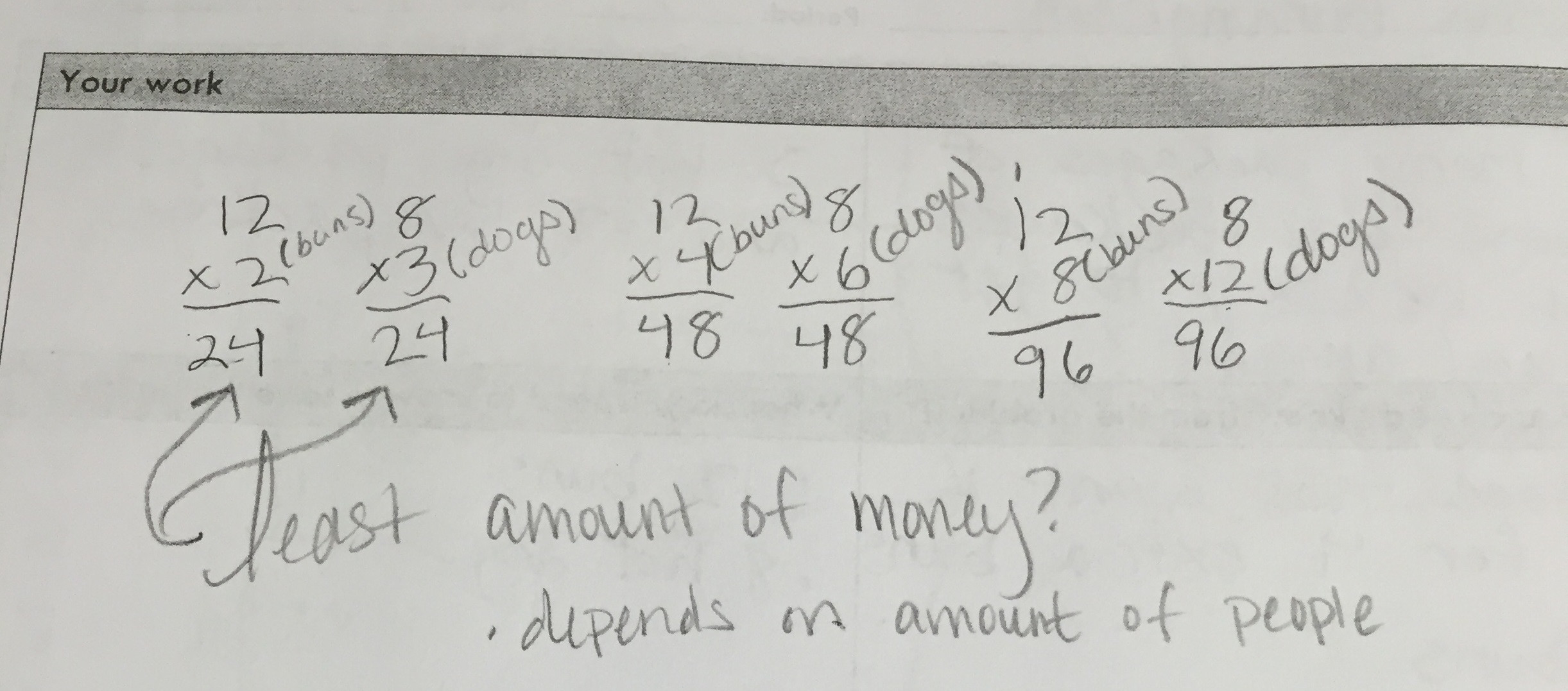student work showing 24 as the least common multiple
Student sample #7:
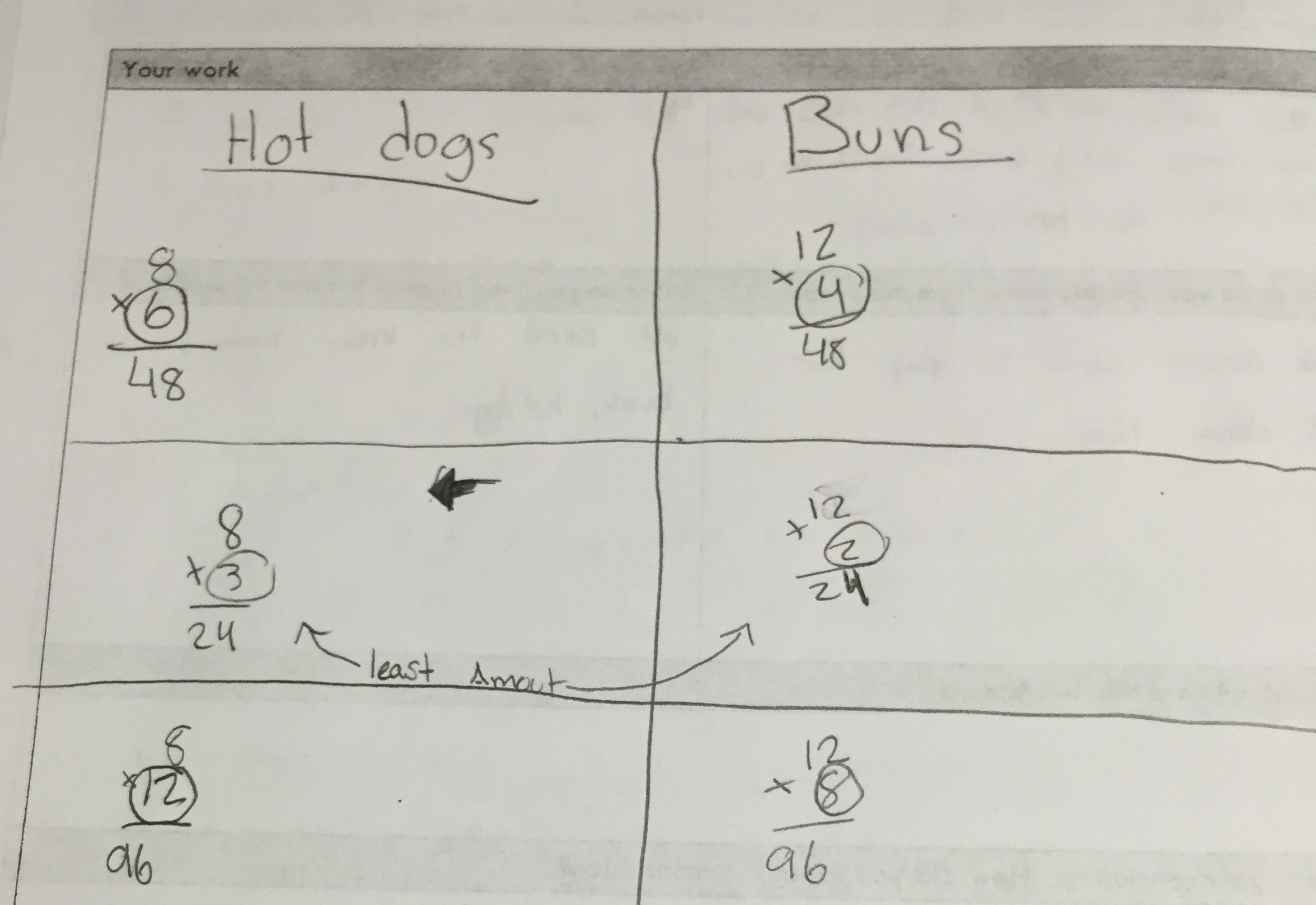student work showing LCM and packages needed
To conclude the lesson, I told them, “Wow, this is incredibly insightful! If I were George Banks, I’d also want to avoid wasting food and spend as little as possible. What you’ve just figured out is a concept you and your teacher will explore further tomorrow, and it’s called the *least common multiple**.*”
Yes, I then used my Expo marker as a microphone and performed a “mic drop” right before the bell rang. I was ecstatic! It was truly one of my most memorable teaching days. This success fueled my excitement for the upcoming third class. Knowing the lesson’s potential, I made a few final tweaks.
Third Attempt: The Charm of Refinement and Focusing the Question
Here was my refined plan for the third class:
- Continue providing the movie background for context.
- Begin with the focused questions: “Why is George so upset?” and “What would happen if he bought just one package of each item?”
- Instead of asking “How many packages should he buy?” I changed the question to “*Okay, let’s investigate how many packages of hot dogs and buns he could buy?*” This subtle shift aimed to encourage exploration of multiple possibilities from the outset.
- Maintain the Problem Solving Framework.
- Allow independent problem-solving time.
- Follow up with the question: “*Knowing what you know about George Banks, how many packages of each should he buy?*” This question now served to refine their thinking after exploring multiple options.
- Conclude by explicitly linking their findings to the concept of least common multiple.
The third class was phenomenal, exceeding even my heightened expectations. Simply changing “should” to “could” in the initial question made a significant difference. It prompted students to think more broadly about various scenarios. The saying “Third time’s a charm” definitely resonated with this experience. Here are examples of student work from this class:
Student sample #8:
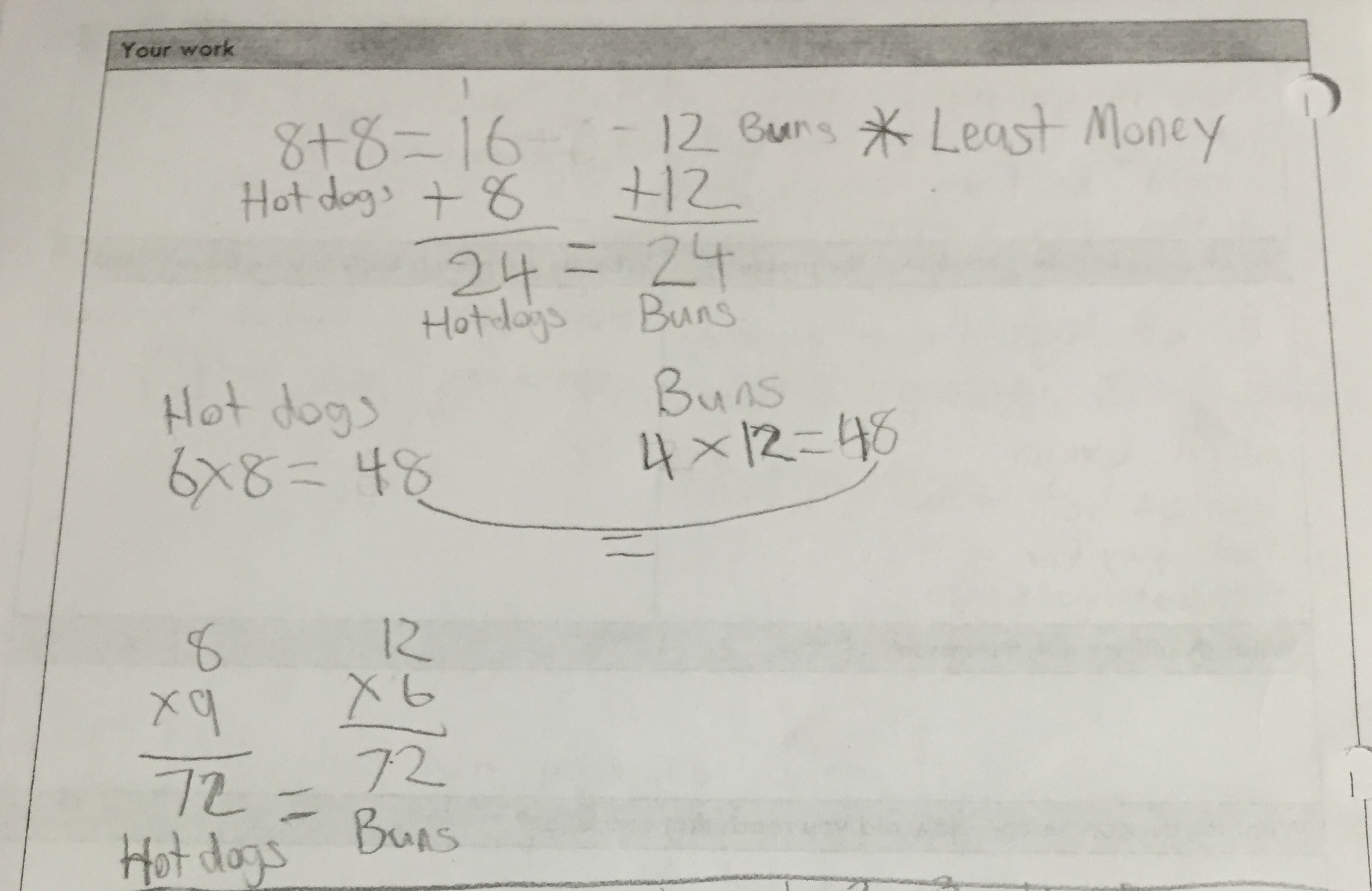student work listing multiples in an organized way
Student sample #9:
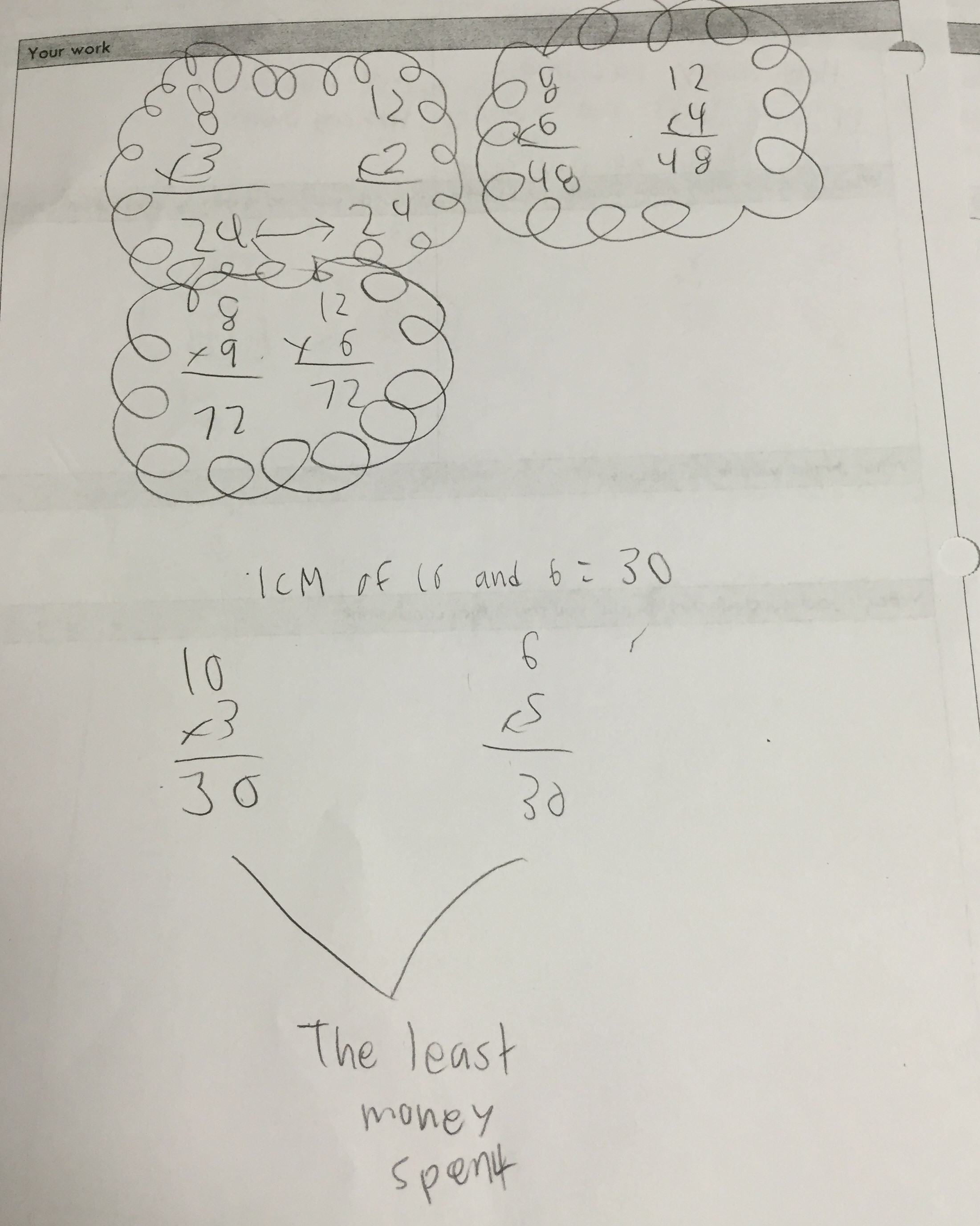student work with clear calculations and LCM identified
(The work at the bottom of this sample relates to the extension question about 10 hot dogs and 6 buns per package)
Student sample #10:
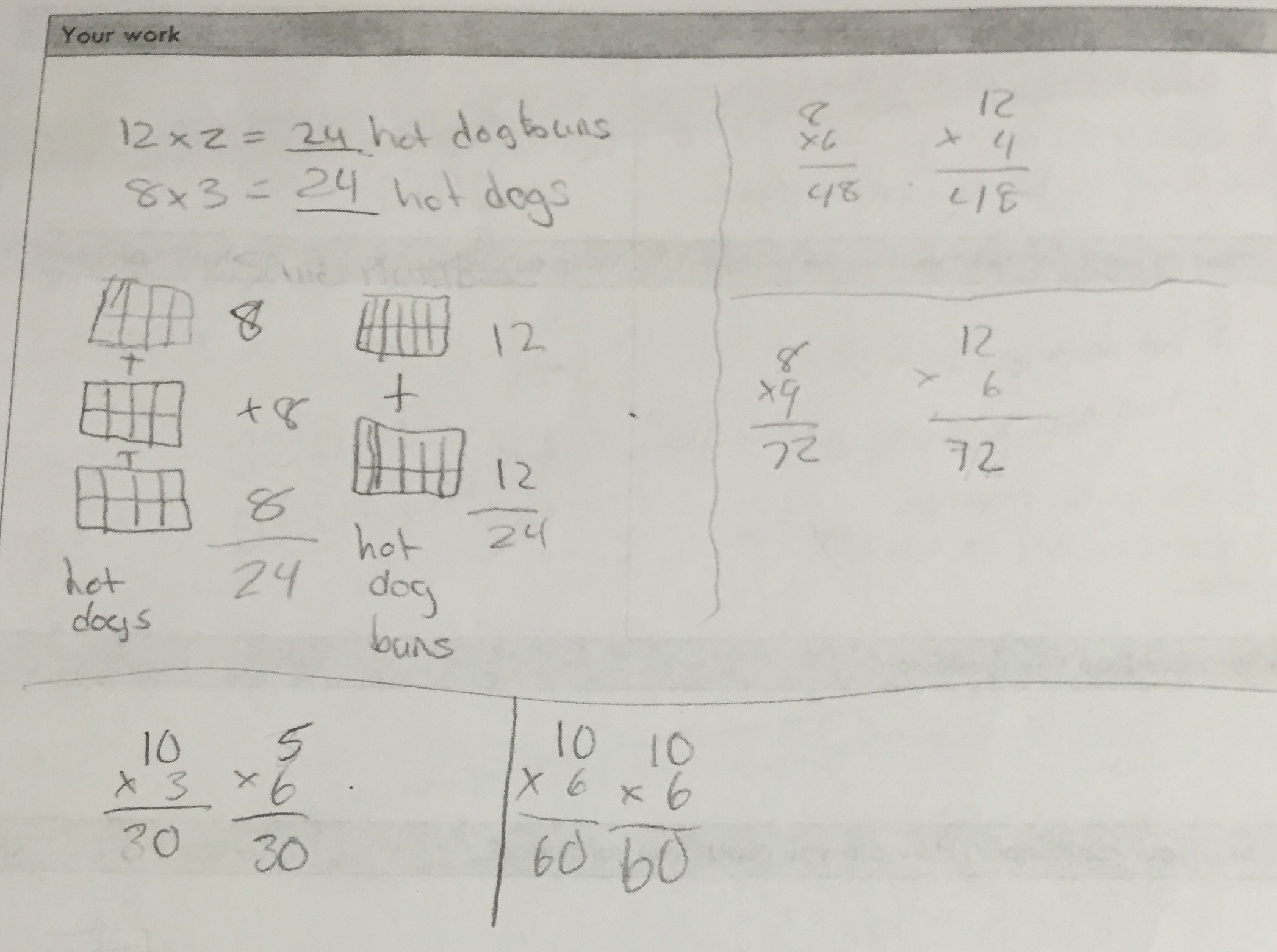student work showing multiple LCM solutions
Student sample #11:
student work showing detailed listing of multiples and packages
(I think this student truly excelled…)
Key Takeaways from This Lesson
- Lesson Recommendation: I wholeheartedly encourage teachers to use this lesson as an engaging introduction to the least common multiple. (Be sure to check out Robert’s recent blog post discussing the crucial aspect of why we select specific math problems for our classrooms – it’s a valuable read). Many students naturally developed strategies that directly mirrored the formal methods the teacher planned to introduce the following day.
- Questioning Strategy: I recommend starting with the question, “How many packages of hot dogs and hot dog buns could he buy?” Then, follow up with, “How many packages of hot dogs and hot dog buns should he buy?” This progression helps students explore the solution space before focusing on the most practical answer.
- Formalization is Key: It is essential for the teacher to dedicate time at the end of the activity to formally introduce the term “least common multiple” to students. This should occur after students have had the opportunity to discuss and justify which scenario George Banks would likely prefer and why. This contextual understanding makes the abstract concept more meaningful.
I truly believe in the power of this lesson. I had an amazing time teaching it, and it proved to be a fantastic activity for the beginning of the school year. Once again, I can’t recommend Robert’s website and blog enough. Explore his resources, try his lessons – you will undoubtedly benefit from his work and insights, just as I have.
For those about to rock in the classroom, we salute you! m/ m/
